Учащимся старших классов будет полезно научиться решать задачи ЕГЭ на нахождение объема и других неизвестных параметров прямоугольного параллелепипеда. Опыт предыдущих лет подтверждает тот факт, что подобные задания являются для многих выпускников достаточно сложными.
При этом понимать, как найти объем или площадь прямоугольного параллелепипеда, должны старшеклассники с любым уровнем подготовки. Только в этом случае они смогут рассчитывать на получение конкурентных баллов по итогам сдачи единого госэкзамена по математике.
Основные нюансы, которые стоит запомнить
- Параллелограммы, из которых состоит параллелепипед, являются его гранями, их стороны - ребрами. Вершины этих фигур считаются вершинами самого многогранника.
- Все диагонали прямоугольного параллелепипеда равны. Так как это прямой многогранник, то боковые грани представляют собой прямоугольники.
- Так как параллелепипед - это призма, в основании которой находится параллелограмм, эта фигура обладает всеми свойствами призмы.
- Боковые ребра прямоугольного параллелепипеда перпендикулярны основанию. Следовательно, они являются его высотами.
Готовьтесь к ЕГЭ вместе со «Школково»!
Чтобы занятия проходили легко и максимально эффективно, выбирайте наш математический портал. Здесь вы найдете весь необходимый материал, который потребуется на этапе подготовки к единому государственному экзамену.
Специалисты образовательного проекта «Школково» предлагают пойти от простого к сложному: сначала мы даем теорию, основные формулы и элементарные задачи с решением, а затем постепенно переходим к заданиям экспертного уровня. Вы можете потренироваться, например, с .
Нужную базовую информацию вы найдете в разделе «Теоретическая справка». Вы также можете сразу приступить к решению задач по теме «Прямоугольный параллелепипед» в онлайн-режиме. В разделе «Каталог» представлена большая подборка упражнений разной степени сложности. База заданий регулярно пополняется.
Проверьте, легко ли вы сможете найти объем прямоугольного параллелепипеда, прямо сейчас. Разберите любое задание. Если упражнение дается вам легко, переходите к более сложным задачам. А если возникли определенные сложности, рекомендуем вам планировать свой день таким образом, чтобы ваше расписание включало занятия с дистанционным порталом «Школково».
Теорема. Во всяком параллелепипеде противоположные грани равны и параллельны.
Так, грани (рис.) BB 1 С 1 С и AA 1 D 1 D параллельны, потому, что две пересекающиеся прямые BB 1 и B 1 С 1 одной грани параллельны двум пересекающимся прямым AA 1 и A 1 D 1 другой. Эти грани и равны, так как B 1 С 1 =A 1 D 1 , B 1 B=A 1 A (как противоположные стороны параллелограммов) и ∠BB 1 С 1 = ∠AA 1 D 1 .
Теорема. Во всяком параллелепипеде все четыре диагонали пересекаются в одной точке и делятся в ней пополам.

Возьмем (рис.) в параллелепипеде какие-нибудь две диагонали, например, AС 1 и DB 1 , и проведем прямые AB 1 и DС 1 .
Так как ребра AD и B 1 С 1 соответственно равны и параллельны ребру BС, то они равны и параллельны между собой.
Вследствие этого фигура ADС 1 B 1 есть параллелограмм, в котором С 1 A и DB 1 - диагонали, а в параллелограмме диагонали пересекаются пополам.
Это доказательство можно повторить о каждых двух диагоналях.
Поэтому диагональ AC 1 пересекается с BD 1 пополам, диагональ BD 1 с A 1 С пополам.
Таким образом, все диагонали пересекаются пополам и, следовательно, в одной точке.
Теорема. В прямоугольном параллелепипеде квадрат любой диагонали равен сумме квадратов трех его измерений.

Пусть (рис.) AC 1 есть какая-нибудь диагональ прямоугольного параллелепипеда.
Проведя AC, получим два треугольника: AC 1 С и ACB. Оба они прямоугольные:
первый потому, что параллелепипед прямой, и следовательно, ребро СС 1 перпендикулярно к основанию,
второй потому, что параллелепипед прямоугольный, значит в основании его лежит прямоугольник.
Из этих треугольников находим:
AC 2 1 = AC 2 + СС 2 1 и AC 2 = AB 2 + BC 2
Следовательно, AC 2 1 = AB 2 + BC 2 + СС 2 1 = AB 2 + AD 2 + AA 2 1
Следствие. В прямоугольном параллелепипеде все диагонали равны .
В геометрии различают такие виды параллелепипедов: прямоугольный параллелепипед (гранями параллелепипеда выступают прямоугольники); прямой параллелепипед (его боковые грани выступают в роли прямоугольников); наклонный параллелепипед (его боковые грани выступают в роли перпендикуляров); куб параллелепипед с абсолютно одинаковыми измерениями, а грани куба - это квадраты. Параллелепипеды могут быть как наклонными, так и прямыми.
Основные элементы параллелепипеда — это то, что две грани представленной геометрической фигуры, которые не имеют общее ребро, являются противоположными, а те которые имеют — смежными. Вершины параллелепипеда, которые не относятся к одной грани, выступают противоположными относительно друг к другу. Параллелепипед имеет измерение — это три ребра, которые имеют общую вершину.
Отрезок, который соединяет противоположные вершины, называется диагональю. Четыре диагонали параллелепипеда, пересекаясь в одной точке, одновременно делятся пополам.
Для того чтобы определить диагональ параллелепипеда, нужно определить стороны и ребра, которые известны по условию задачи. При известных трех ребрах А , В , С проведите в параллелепипеде диагональ. Согласно свойству параллелепипеда, которое говорит о том, что все углы его прямые, определяется диагональ. Построить диагональ от одной из граней параллелепипеда. Диагонали нужно проводить таким образом, чтобы диагональ грани, искомая диагональ параллелепипеда и известное ребро, создавали треугольник. После того как образуется треугольник, найдите длину данной диагонали. Диагональ в другом полученном треугольнике выступает в роли гипотенузы, поэтому ее можно найти по теореме Пифагора, которую необходимо взять под корень квадратный. Таким образом, мы узнаем значение второй диагонали. Для того чтобы найти первую диагональ параллелепипеда в образованном прямоугольном треугольнике, также необходимо отыскать неизвестную гипотенузу (за теоремой Пифагора). По такому же примеру последовательно найдите остальные три существующие в параллелепипеде диагонали, выполнив дополнительные построения диагоналей, которые образуют прямоугольные треугольники и решите по теореме Пифагора.
Прямоугольным параллелепипедом (ПП) является ни что иное, как призма, основанием у которой прямоугольник. У ПП все диагонали равны, значит любая его диагональ рассчитывается по формуле:
а, в — стороны основания ПП;
с — его высота.
Можно дать и другое определение, рассматривая декартову прямоугольную систему координат:
Диагональ ПП это радиус-вектор любой точки пространства, заданной координатами x, y и z в декартовой системе координат. Этот радиус вектор к точке проводится из начала координат. А координатами точки будут проекции радиус-вектора (диагонали ПП) на координатные оси.
1055;роекции совпадают с вершинами данного параллелепипеда.
Параллелепипед и его виды
Если дословно перевести его название с древнегреческого, то получится, что это фигура, состоящая из параллельных плоскостей. Существуют такие равносильные определения параллелепипеда:
- призма с основанием в виде параллелограмма;
- многогранник, каждая грань которого — параллелограмм.
Его виды выделяются в зависимости от того, какая фигура лежит в его основании и как направлены боковые ребра. В общем случае говорят о наклонном параллелепипеде , у которого основание и все грани — параллелограммы. Если у предыдущего вида боковые грани станут прямоугольниками, то его нужно будет называть уже прямым . А у прямоугольного и основание тоже имеет углы по 90º.

Причем последний в геометрии стараются изображать так, чтобы было заметно, что все ребра параллельны. Здесь, кстати, наблюдается основное отличие математиков от художников. Последним важно передать тело с соблюдением закона перспективы. И в этом случае параллельность ребер совсем незаметна.

О введенных обозначениях
В приведенных ниже формулах справедливы обозначения, указанные в таблице.
Формулы для наклонного параллелепипеда
Первая и вторая для площадей:
Третья для того, чтобы вычислить объем параллелепипеда:
Так как основание — параллелограмм, то для расчета его площади нужно будет воспользоваться соответствующими выражениями.

Формулы для прямоугольного параллелепипеда
Аналогично первому пункту — две формулы для площадей:
И еще одна для объема:
Первая задача
Условие. Дан прямоугольный параллелепипед, объем которого требуется найти. Известна диагональ — 18 см — и то, что она образует углы в 30 и 45 градусов с плоскостью боковой грани и боковым ребром соответственно.
Решение. Чтобы ответить на вопрос задачи, потребуется узнать все стороны в трех прямоугольных треугольниках. Они дадут необходимые значения ребер, по которым нужно сосчитать объем.
Сначала нужно выяснить, где находится угол в 30º. Для этого нужно провести диагональ боковой грани из той же вершины, откуда чертилась главная диагональ параллелограмма. Угол между ними и будет тем, что нужен.
Первый треугольник, который даст одно из значений сторон основания, будет следующим. В нем содержатся искомая сторона и две проведенные диагонали. Он прямоугольный. Теперь потребуется воспользоваться отношением противолежащего катета (стороны основания) и гипотенузы (диагонали). Оно равно синусу 30º. То есть неизвестная сторона основания будет определяться как диагональ, умноженная на синус 30º или ½. Пусть она будет обозначена буквой «а».
Вторым будет треугольник, содержащий известную диагональ и ребро, с которым она образует 45º. Он тоже прямоугольный, и можно опять воспользоваться отношением катета к гипотенузе. Другими словами, бокового ребра к диагонали. Оно равно косинусу 45º. То есть «с» вычисляется как произведение диагонали на косинус 45º.
с = 18 * 1/√2 = 9 √2 (см).
В этом же треугольнике требуется найти другой катет. Это необходимо для того, чтобы потом сосчитать третью неизвестную — «в». Пусть она будет обозначена буквой «х». Ее легко вычислить по теореме Пифагора:
х = √(18 2 — (9√2) 2) = 9√2 (см).
Теперь нужно рассмотреть еще один прямоугольный треугольник. Он содержит уже известные стороны «с», «х» и ту, что нужно сосчитать, «в»:
в = √((9√2) 2 — 9 2 = 9 (см).
Все три величины известны. Можно воспользоваться формулой для объема и сосчитать его:
V = 9 * 9 * 9√2 = 729√2 (см 3).
Ответ: объем параллелепипеда равен 729√2 см 3 .

Вторая задача
Условие. Требуется найти объем параллелепипеда. В нем известны стороны параллелограмма, который лежит в основании, 3 и 6 см, а также его острый угол — 45º. Боковое ребро имеет наклон к основанию в 30º и равно 4 см.
Решение. Для ответа на вопрос задачи нужно взять формулу, которая была записана для объема наклонного параллелепипеда. Но в ней неизвестны обе величины.
Площадь основания, то есть параллелограмма, будет определена по формуле, в которой нужно перемножить известные стороны и синус острого угла между ними.
S о = 3 * 6 sin 45º = 18 * (√2)/2 = 9 √2 (см 2).
Вторая неизвестная величина — это высота. Ее можно провести из любой из четырех вершин над основанием. Ее найти можно из прямоугольного треугольника, в котором высота является катетом, а боковое ребро — гипотенузой. При этом угол в 30º лежит напротив неизвестной высоты. Значит, можно воспользоваться отношением катета к гипотенузе.
н = 4 * sin 30º = 4 * 1/2 = 2.
Теперь все значения известны и можно вычислить объем:
V = 9 √2 * 2 = 18 √2 (см 3).
Ответ: объем равен 18 √2 см 3 .

Третья задача
Условие. Найти объем параллелепипеда, если известно, что он прямой. Стороны его основания образуют параллелограмм и равны 2 и 3 см. Острый угол между ними 60º. Меньшая диагональ параллелепипеда равна большей диагонали основания.
Решение. Для того чтобы узнать объем параллелепипеда, воспользуемся формулой с площадью основания и высотой. Обе величины неизвестны, но их несложно вычислить. Первая из них высота.
Поскольку меньшая диагональ параллелепипеда совпадает по размеру с большей основания, то их можно обозначить одной буквой d. Больший угол параллелограмма равен 120º, поскольку с острым он образует 180º. Пусть вторая диагональ основания будет обозначена буквой «х». Теперь для двух диагоналей основания можно записать теоремы косинусов:
d 2 = а 2 + в 2 — 2ав cos 120º,
х 2 = а 2 + в 2 — 2ав cos 60º.
Находить значения без квадратов не имеет смысла, так как потом они будут снова возведены во вторую степень. После подстановки данных получается:
d 2 = 2 2 + 3 2 — 2 * 2 * 3 cos 120º = 4 + 9 + 12 * ½ = 19,
х 2 = а 2 + в 2 — 2ав cos 60º = 4 + 9 — 12 * ½ = 7.
Теперь высота, она же боковое ребро параллелепипеда, окажется катетом в треугольнике. Гипотенузой будет известная диагональ тела, а вторым катетом — «х». Можно записать Теорему Пифагора:
н 2 = d 2 — х 2 = 19 — 7 = 12.
Отсюда: н = √12 = 2√3 (см).
Теперь вторая неизвестная величина — площадь основания. Ее можно сосчитать по формуле, упомянутой во второй задаче.
S о = 2 * 3 sin 60º = 6 * √3/2 = 3√3 (см 2).
Объединив все в формулу объема, получаем:
V = 3√3 * 2√3 = 18 (см 3).
Ответ: V = 18 см 3 .

Четвертая задача
Условие. Требуется узнать объем параллелепипеда, отвечающего таким условиям: основание — квадрат со стороной 5 см; боковые грани являются ромбами; одна из вершин, находящихся над основанием, равноудалена от всех вершин, лежащих в основании.
Решение. Сначала нужно разобраться с условием. С первым пунктом про квадрат вопросов нет. Второй, про ромбы, дает понять, что параллелепипед наклонный. Причем все его ребра равны 5 см, поскольку стороны у ромба одинаковые. А из третьего становится ясно, что три диагонали, проведенные из нее, равны. Это две, которые лежат на боковых гранях, а последняя внутри параллелепипеда. И эти диагонали равны ребру, то есть тоже имеют длину 5 см.
Для определения объема будет нужна формула, записанная для наклонного параллелепипеда. В ней опять нет известных величин. Однако площадь основания вычислить легко, потому что это квадрат.
S о = 5 2 = 25 (см 2).
Немного сложнее обстоит дело с высотой. Она будет таковой в трех фигурах: параллелепипеде, четырехугольной пирамиде и равнобедренном треугольнике. Последним обстоятельством и нужно воспользоваться.
Поскольку она высота, то является катетом в прямоугольном треугольнике. Гипотенузой в нем будет известное ребро, а второй катет равен половине диагонали квадрата (высота — она же и медиана). А диагональ основания найти просто:
d = √(2 * 5 2) = 5√2 (см).
н = √ (5 2 — (5/2 * √2) 2) = √(25 — 25/2) = √(25/2) = 2,5 √2 (см).
V = 25 * 2,5 √2 = 62,5 √2 (см 3).
Ответ: 62,5 √2 (см 3).
На этом уроке все желающие смогут изучить тему «Прямоугольный параллелепипед». В начале урока мы повторим, что такое произвольный и прямой параллелепипеды, вспомним свойства их противоположных граней и диагоналей параллелепипеда. Затем рассмотрим, что такое прямоугольный параллелепипед, и обсудим его основные свойства.
Тема: Перпендикулярность прямых и плоскостей
Урок: Прямоугольный параллелепипед
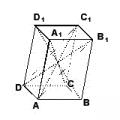
Поверхность, составленная из двух равных параллелограммов АВСD и А 1 В 1 С 1 D 1 и четырех параллелограммов АВВ 1 А 1 , ВСС 1 В 1 , СDD 1 С 1 , DАА 1 D 1 , называется параллелепипедом (рис. 1).
Рис. 1 Параллелепипед
То есть: имеем два равных параллелограмма АВСD и А 1 В 1 С 1 D 1 (основания), они лежат в параллельных плоскостях так, что боковые ребра АА 1 , ВВ 1 , DD 1 , СС 1 параллельны. Таким образом, составленная из параллелограммов поверхность называется параллелепипедом .
Таким образом, поверхность параллелепипеда - это сумма всех параллелограммов, из которых составлен параллелепипед.
1. Противоположные грани параллелепипеда параллельны и равны.
(фигуры равны, то есть их можно совместить наложением)
Например:
АВСD = А 1 В 1 С 1 D 1 (равные параллелограммы по определению),
АА 1 В 1 В = DD 1 С 1 С (так как АА 1 В 1 В и DD 1 С 1 С - противоположные грани параллелепипеда),
АА 1 D 1 D = ВВ 1 С 1 С (так как АА 1 D 1 D и ВВ 1 С 1 С - противоположные грани параллелепипеда).
2. Диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.
Диагонали параллелепипеда АС 1 , В 1 D, А 1 С, D 1 В пересекаются в одной точке О, и каждая диагональ делится этой точкой пополам (рис. 2).

Рис. 2 Диагонали параллелепипеда пересекаются и деляться точкой пересечения пополам.
3. Имеются три четверки равных и параллельных ребер параллелепипеда : 1 - АВ, А 1 В 1 , D 1 C 1 , DC, 2 - AD, A 1 D 1 , B 1 C 1 , BC, 3 - АА 1 , ВВ 1 , СС 1 , DD 1 .
Определение. Параллелепипед называется прямым, если его боковые ребра перпендикулярны основаниям.
Пусть боковое ребро АА 1 перпендикулярно основанию (рис. 3). Это означает, что прямая АА 1 перпендикулярна прямым АD и АВ, которые лежат в плоскости основания. А, значит, в боковых гранях лежат прямоугольники. А в основаниях лежат произвольные параллелограммы. Обозначим, ∠BAD = φ, угол φ может быть любым.

Рис. 3 Прямой параллелепипед
Итак, прямой параллелепипед - это параллелепипед, в котором боковые ребра перпендикулярны основаниям параллелепипеда.
Определение. Параллелепипед называется прямоугольным, если его боковые ребра перпендикулярны к основанию. Основания являются прямоугольниками.
Параллелепипед АВСDА 1 В 1 С 1 D 1 - прямоугольный (рис. 4), если:
1. АА 1 ⊥ АВСD (боковое ребро перпендикулярно плоскости основания, то есть параллелепипед прямой).
2. ∠ВАD = 90°, т. е. в основании лежит прямоугольник.

Рис. 4 Прямоугольный параллелепипед
Прямоугольный параллелепипед обладает всеми свойствами произвольного параллелепипеда. Но есть дополнительные свойства, которые выводятся из определения прямоугольного параллелепипеда.
Итак, прямоугольный параллелепипед - это параллелепипед, у которого боковые ребра перпендикулярны основанию. Основание прямоугольного параллелепипеда - прямоугольник .
1. В прямоугольном параллелепипеде все шесть граней прямоугольники.
АВСD и А 1 В 1 С 1 D 1 - прямоугольники по определению.
2. Боковые ребра перпендикулярны основанию . Значит, все боковые грани прямоугольного параллелепипеда - прямоугольники.
3. Все двугранные углы прямоугольного параллелепипеда прямые.
Рассмотрим, например, двугранный угол прямоугольного параллелепипеда с ребром АВ, т. е. двугранный угол между плоскостями АВВ 1 и АВС.
АВ - ребро, точка А 1 лежит в одной плоскости - в плоскости АВВ 1 , а точка D в другой - в плоскости А 1 В 1 С 1 D 1 . Тогда рассматриваемый двугранный угол можно еще обозначить следующим образом: ∠А 1 АВD.
Возьмем точку А на ребре АВ. АА 1 - перпендикуляр к ребру АВ в плоскости АВВ- 1 , AD перпендикуляр к ребру АВ в плоскости АВС. Значит, ∠А 1 АD - линейный угол данного двугранного угла. ∠А 1 АD = 90°, значит, двугранный угол при ребре АВ равен 90°.
∠(АВВ 1 , АВС) = ∠(АВ) = ∠А 1 АВD= ∠А 1 АD = 90°.
Аналогично доказывается, что любые двугранные углы прямоугольного параллелепипеда прямые.
Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений.
Примечание. Длины трех ребер, исходящих из одной вершины прямоугольного параллелепипеда, являются измерениями прямоугольного параллелепипеда. Их иногда называют длина, ширина, высота.
Дано: АВСDА 1 В 1 С 1 D 1 - прямоугольный параллелепипед (рис. 5).
Доказать: .

Рис. 5 Прямоугольный параллелепипед
Доказательство:
Прямая СС 1 перпендикулярна плоскости АВС, а значит, и прямой АС. Значит, треугольник СС 1 А - прямоугольный. По теореме Пифагора:
![]()
Рассмотрим прямоугольный треугольник АВС. По теореме Пифагора:
![]()
Но ВС и AD - противоположные стороны прямоугольника. Значит, ВС = AD. Тогда:
![]()
Так как ![]() , а
, а ![]() , то. Поскольку СС 1 = АА 1 , то что и требовалось доказать.
, то. Поскольку СС 1 = АА 1 , то что и требовалось доказать.
Диагонали прямоугольного параллелепипеда равны.
Обозначим измерения параллелепипеда АВС как a, b, c (см. рис. 6), тогда АС 1 = СА 1 = В 1 D = DВ 1 =

Параллелепипед – это геометрическая фигура, все 6 граней которой представляют собой параллелограммы.
В зависимости от вида этих параллелограммов различают следующие виды параллелепипеда:
- прямой;
- наклонный;
- прямоугольный.
Прямым параллелепипедом называют четырехугольную призму, ребра которой составляют с плоскостью основания угол 90 °.
Прямоугольным параллелепипедом называют четырехугольную призму, все грани которой являются прямоугольниками. Куб есть разновидность четырехугольной призмы, у которой все грани и ребра равны между собой.
Особенности фигуры предопределяют ее свойства. К ним относят 4 следующих утверждений:

Запомнить все приведенные свойства просто, они легки для понимания и выводятся логически исходя из вида и особенностей геометрического тела. Однако, незамысловатые утверждения могут быть невероятно полезны при решении типовых заданий ЕГЭ и позволят сэкономить время необходимое для прохождения теста.
Формулы параллелепипеда
Для поиска ответов на поставленную задачу недостаточно знать только свойства фигуры. Также могут понадобиться и некоторые формулы для нахождения площади и объема геометрического тела.

Площадь оснований находится также как и соответствующий показатель параллелограмма или прямоугольника. Выбирать основание параллелограмма можно самостоятельно. Как правило, при решении задач проще работать с призмой, в основании которой лежит прямоугольник.
Формула нахождения боковой поверхности параллелепипеда, также может понадобиться в тестовых заданиях.

Примеры решения типовых заданий ЕГЭ
Задание 1.
Дано
: прямоугольный параллелепипед с измерениями 3, 4 и 12 см.
Необходимо
найти длину одной из главных диагоналей фигуры.
Решение
: Любое решение геометрической задачи должно начинаться с построения правильного и четкого чертежа, на котором будет обозначено «дано» и искомая величина. На рисунке ниже приведен пример правильного оформления условий задания.

Рассмотрев сделанный рисунок и вспомнив все свойства геометрического тела, приходим к единственно верному способу решения. Применив 4 свойство параллелепипеда, получим следующее выражение:

После несложных вычислений получим выражение b2=169, следовательно, b=13. Ответ задания найден, на его поиск и чертеж необходимо потратить не более 5 минут.